자료구조 해쉬테이블(HashTable)
resilient
·2021. 5. 28. 10:34
컴퓨터는 어쨌든 숫자로 이루어져있고 숫자로 모든작업을 수행한다. 이를 이용해서 특정 데이터를 찾을 때 숫자를 이용한 인덱스로 메모리의 위치에서 데이터를 가져올 수 있다.
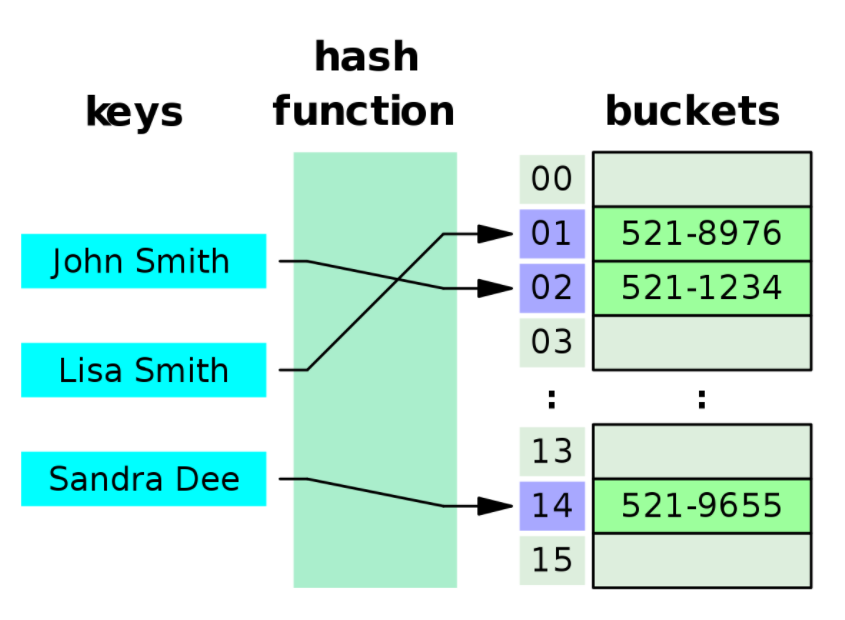
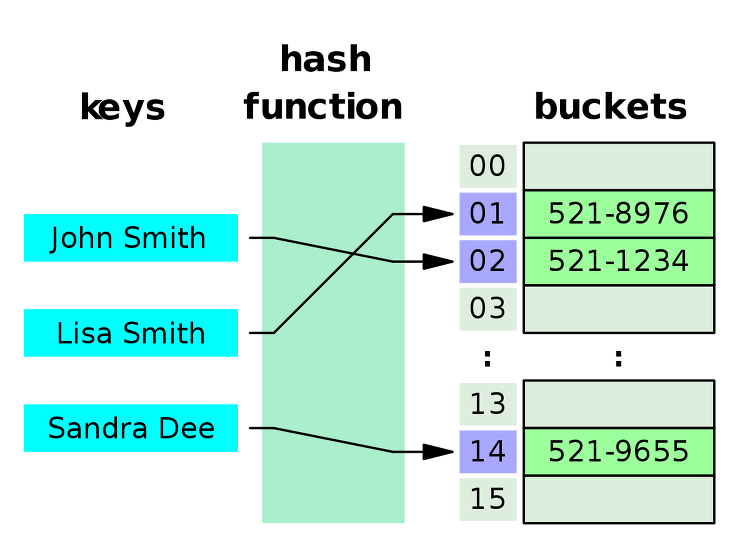
해쉬 테이블이란?
해시 테이블은 키(Key), 해시함수(Hash Function), 해시(Hash), 값(value), 저장소(Bucket, Slot)로 이루어져 있다.
해쉬 테이블은 key-value 쌍에서 key 값을 테이블에 저장할 때 데이터를 직접 넣는 방법과는 다르게 key(숫자) 값을 Hash함수를 이용해 계산을 수행한 후, 결과값을 테이블에 넣는 것이다.
Hash함수는 입력으로 key값을 받고, 0부터 (배열의 크기-1) 사이의 값을 출력해준다. 이 경우 k값이 h(k)로 해쉬되었다고 하고, h(k)는 k의 해쉬값 이라고 한다.
예를 들어 위에 그림과 같은 hash함수가 있다고 가정했을 때, John Smith라는 string 데이터를 직접 넘기지 않고
521-8976번 버켓의 1번으로 변환을 해서 데이터를 넘기는 방식이다.
(여기서 버켓(Bucket)은 저장소를 의미한다.)
간단한 예시를 들어보면, division method(나머지방법)이 있다.
알파벳 A,B,C,D 를 해쉬테이블에 저장하려고 할 때, 아스키 값으로 바꾸면,65,66,67,68이다. 버켓이 10개라고 가정했을 때, 10개의 버켓에 나누어 넣는방법은 10으로 나눈 나머지로 생각할 수 있다.
A의 아스키값인 65는 5번 버켓으로, B는 6번, C는 7번, D는 8번으로 보내면 간단한 해쉬함수를 이용한 해쉬 테이블 생성이 완료된 것이다.
해시테이블을 파이썬으로 구현해 보았다.(Division method)
from collections import defaultdict
import collections
# 단일연결리스트 생성
class ListNode:
def __init__(self, key=None, value=None):
self.key = key
self.value = value
self.next = None
# 해시맵 사이즈는 1000으로 설정
HASHMAP_SIZE = 1000
class MyHashMap:
# 초기화
def __init__(self):
self.size = HASHMAP_SIZE
self.table = defaultdict(ListNode)
# def _hash()
# 삽입
def put(self, key: int, value: int) -> None:
index = key % self.size
# index 값이 비어져 있을 때
if self.table[index].value is None:
self.table[index] = ListNode(key, value)
return
# index 값이 채워져 있을 때
p = self.table[index]
while p: # p == None -->
if p.key == key:
p.value = value
return
if p.next is None:
break
p = p.next
p.next = ListNode(key, value)
# 조회
def get(self, key: int) -> int:
index = key % self.size
# 비어 있다면
if self.table[index].value is None:
return -1
# 링크드 리스트가 있다면
p = self.table[index]
while p:
if p.key == key:
return p.value
p = p.next
return -1
# 삭제
def remove(self, key: int) -> None:
index = key % self.size
# 비어있는 경우
if self.table[index].value is None:
return
# 링크드리스트의 첫번째, head
p = self.table[index]
if p.key == key:
self.table[index] = ListNode() if p.next is None else p.next
return
# 중간에 있는 경우에는, 전, 다음꺼를 연결해주는 경우
prev = p
while p:
if p.key == key:
prev.next = p.next
return
prev, p = p, p.nextHash Collision(해시 충돌)
해시 테이블을 Insertion, Deletion,Search 과정에서 모두 O(1)의 시간복잡도, 최대 O(n)의 시간복잡도를 가지고 있다.
하지만 해시를 이용한 자료구조 방식에 있을 수 밖에 없는 문제는 해시 충돌이다.
무한한 Key값을 유한한 Hash값으로 표현하면서 서로 다른 두개 이상의 유한한 값이 동일한 출력값을 가지게 된다는 것이다.
이를 해결하기 위한 방법으로는 다음과 같은 방법들이 있다.
Seperate Chaining 방법 (충돌의 허용하지만 최소화 하는 방법)

Sandra가 들어가는데 충돌이 일어나니 기존에 있던 John의 값에 연결시켰다.
체이닝(Chaining)은 자료 저장 시, 저장소(bucket)에서 충돌이 일어나면 해당 값을 기존 값과 연결시키는 기법이다.
위의 사진에서 Sandra를 저장할 때 충돌이 일어났고, 기존에 있던 John에 연결시켰다. 이 때 연결리스트(Linked List) 자료구조를 이용한다. 다음에 저장된 자료를 기존의 자료 다음에 위치시키는 것이다.
Chaining 장단점
장점
- 한정된 저장소(Bucket)을 효율적으로 사용할 수 있다.
- 해시 함수(Hash Function)을 선택하는 중요성이 상대적으로 적다.
- 상대적으로 적은 메모리를 사용한다. 미리 공간을 잡아 놓을 필요가 없다.
단점
- 한 Hash에 자료들이 계속 연결된다면(쏠림 현상) 검색 효율을 낮출 수 있다.
- 외부 저장 공간을 사용한다.
- 외부 저장 공간 작업을 추가로 해야 한다.
Open Addressing(개방주소법)
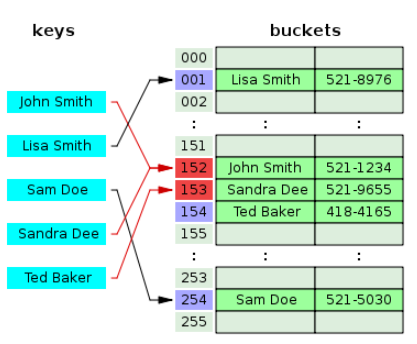
개방주소법은 데이터의 해시(hash)가 변경되지 않았던 chaining과는 달리 비어있는 해시(hash)를 찾아 데이터를 저장하는 기법이다. 따라서 개방주소법에서의 해시테이블은 1개의 해시와 1개의 값(value)가 매칭되어 있는 형태로 유지된다.
위의 그림을 보면, Sandra가 저장될때 해시가 John으로 채워져 있어서 그 다음 Hash에 Sandra를 저장했다. 그리고 Ted의 해시도 Sandra가 저장되어 있으므로 그 다음 해시에 Ted를 저장했다. 이처럼 비어있는 해시를 찾아 저장하는 방법을 Open Addressing라고 한다.
이 때, 비어있는 해시(Hash)를 찾는 과정은 동일해야 한다.(일정한 규칙을 따라 찾아가야 한다.)
Open Addressing는 위에서 언급한 비어있는 해시를 찾는 규칙에 따라 다음과 같이 구분할 수 있다.
- 선형 탐색(Linear Probing): 다음 해시(+1)나 n개(+n)를 건너뛰어 비어있는 해시에 데이터를 저장한다.
- 제곱 탐색(Quadratic Probing): 충돌이 일어난 해시의 제곱을 한 해시에 데이터를 저장한다.
- 이중 해시(Double Hashing): 다른 해시함수를 한 번 더 적용한 해시에 데이터를 저장한다.
Open Addressing의 장단점
장점
- 또 다른 저장공간 없이 해시테이블 내에서 데이터 저장 및 처리가 가능하다.
- 또 다른 저장공간에서의 추가적인 작업이 없다
단점
- 해시 함수(Hash Function)의 성능에 전체 해시테이블의 성능이 좌지우지된다.
- 데이터의 길이가 늘어나면 그에 해당하는 저장소를 마련해 두어야 한다.
'자료구조 & 알고리즘 > 자료구조' 카테고리의 다른 글
| 자료구조에서의 스택(Stack) 이란? (0) | 2021.12.04 |
|---|---|
| 자료구조 트리(Tree) (0) | 2021.05.22 |
| 다익스트라 알고리즘(Dijkstra Algorithm)(feat.힙(heap)) (0) | 2021.05.19 |
| 자료구조 우선순위 큐(Priority Queue)와 힙(heap) (0) | 2021.05.19 |





